如今，随网络信息技术的迅猛发展，以及人们对力学、电学等理工学科研究的不断深入，惯性导航技术也在随之发生着日新月异的变化。在惯性导航系统中，控制技术起着至关重要的作用，目前平台式惯导控制大多采用经典频域控制设计方法。随着控制技术的发展，鲁棒控制理论也得到了极大的发展，它对于控制对象存在不确定性和结构摄动有更好的控制效果。本文采用鲁棒H控制问题转化为H∞ 混合灵敏度问题，运用混合灵敏度优化设计出了一个满足性能要求的控制器，并通过特殊的双线性变换方法，解决了平台原系统对象模型有位于虚轴极点这一病态问题。最后，通过仿真验证了控制器的可行性。

  三轴惯性平台具有三条伺服回路通道，其原理基本相同。当某一干扰力矩M f 作用在平台台体框架轴上时，平台将相对惯性空间产生转动，液浮陀螺敏感到此偏转角度后，输入相应的调宽信号，经过放大器放大后反馈到控制装置，由控制装置产生控制信号作用在稳定电机上，稳定电机产生相反方向的修正力矩，带着平台向着原来偏离的反方向运动，使平台与惯性空间的夹角逐渐减小到0，最终使平台相对于惯性空间保持稳定。

  一般稳定回路由惯性平台、三环框架、安装在平台上的陀螺仪、力矩电机、坐标变换器和控制电路组成。具体组成如图1 所示，其中Md为力矩电机扭转力矩，Mf为稳定回路外部干扰力矩。图1 由横滚稳定回路和俯仰稳定回路组成，方位稳定回路没有耦合放大器和伺服分解器两个环节。

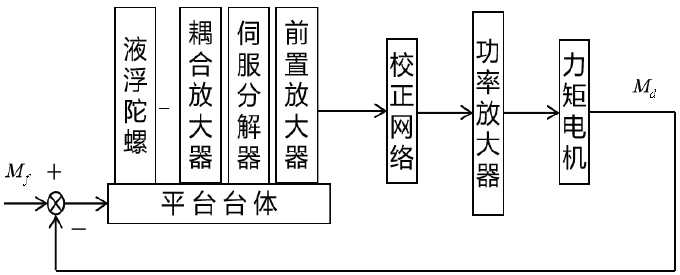
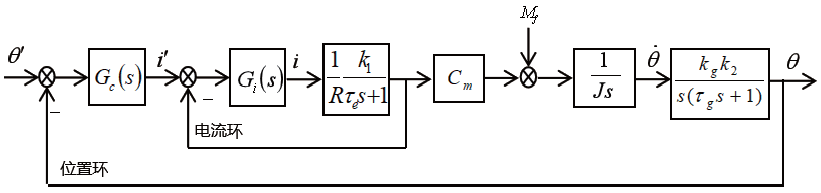
  图2 为方位稳定回路控制框图，其中，θ ′ 为稳定回路输入角度，θ 为陀螺输出角，k1 为桥式功率放大系数，k2 为传感器、前置放大、相敏解调和低通滤波放大系数、τ g 为陀螺时间常数、kg 为陀螺传递系数、τ e 为电机时间常数， J 为平台转动惯量。不考虑校正装置，稳定回路的开环传递函数为

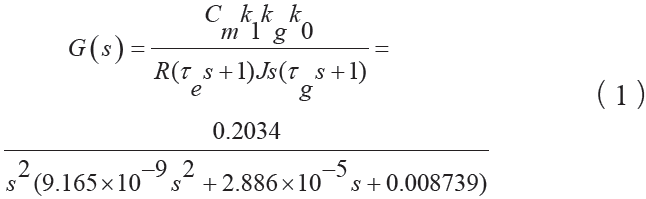
  PID 控制器是控制管理系统中最常使用的一种控制器，具有结构相对比较简单、调整方便、稳定性高及工作可靠等优点。PID 控制主要是依靠被控系统的输出值与目标值之间的偏差和实际经验来实现系统的控制。平台稳定回路通常采取双闭环控制，即电流环PI 控制、位置环PID 控制，控制框图如图2 所示。

  电流环反馈能自动调节力矩电机的驱动电流，大大减小载体角运动和干扰力矩引起的力矩电机输出力矩波动，来提升系统性能。

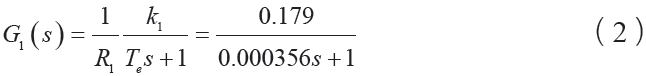
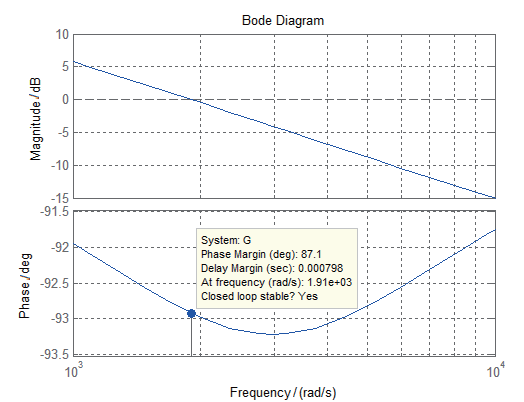
  根据工程的真实的情况，此处取电流环的开环截止频率为 1 800~2 000 rad / s，此时取电流环校正函数为

  控制后开环系统的截止频率为 1 910 rad / s，相位裕度为87.1°。

  PID 控制采用比例- 积分- 微分控制的基本形式。本文位置环PID 校正整定采取临界比例法。

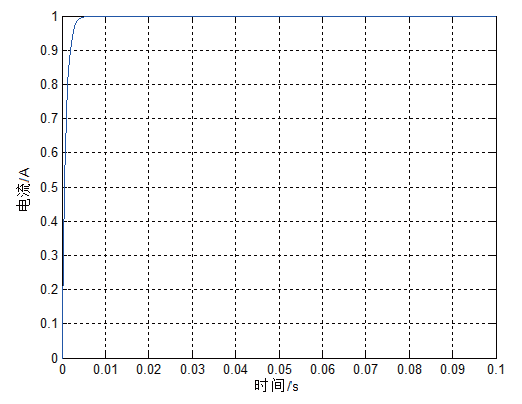
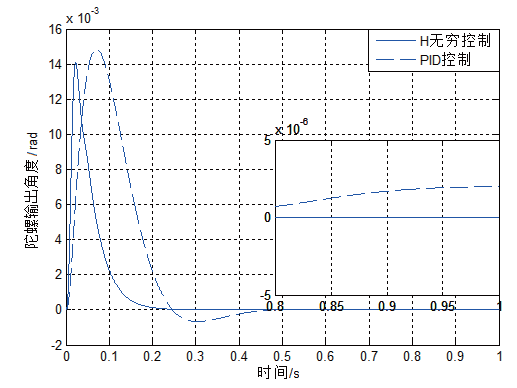
  对PID 控制稳定环回路输入0.1 rad 的阶跃信号和0.5 N·m 的干扰力矩，系统的响应曲线 能够准确的看出，采用常规PID 控制后，系统超调为18.5%，调节时间为0.12 s，当输入常值干扰力矩后，稳定回路的最大动态干扰误差为0.014 9 rad，稳定误差最终趋于0。

  混合灵敏度加权的控制结构如图5 所示，其中r 为参考输入、e 为跟踪误差、u 为控制输入、d 为干扰输入、y为系统输出、G(s)为控制对象、W1、W2

  其中， S 和T 分别被称为灵敏度函数和补灵敏度函数，二者满足：T (s) = I − S (s)。灵敏度函数S (s)是决定跟踪误差大小的重要指标，S (s)增益越低，系统的跟踪误差越小，故系统响应的品质指标越好；而补灵敏度函数T (s)是决定系统鲁棒稳定性的重要指标，降低T (s)增益能减小模型不确定性对系统的影响。但由于T (s) = I − S (s)，不可能同时降低S和T的增益，通常干扰信号多为低频信号，系统不确定性发生高频，因此在选择权函数上可以对二者进行分频段折衷。

  上式右端为目标函数的线性分式变换形式。因此，使系统内部稳定且满足设计指标ψ ∞ 1的控制器K (s)的问题，就可以归结为求增广被控对象G s H( )所对应的H

  在本文中，图5中的G(s)即为力矩电机、平台台体、液浮陀螺三者组成的总被控对象，代入具体数值：

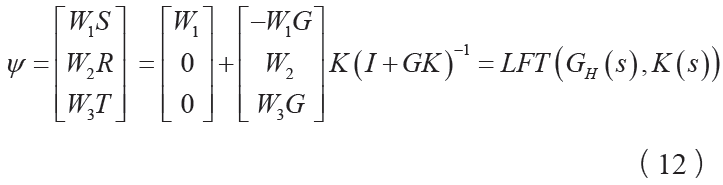
  标准控制结构，如图6 所示。虚线框即为增广对象，它包含原控制对象 G(s) W1 、W2 、W3 三个权函数。

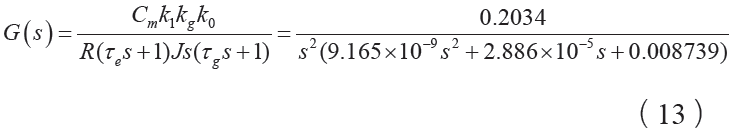
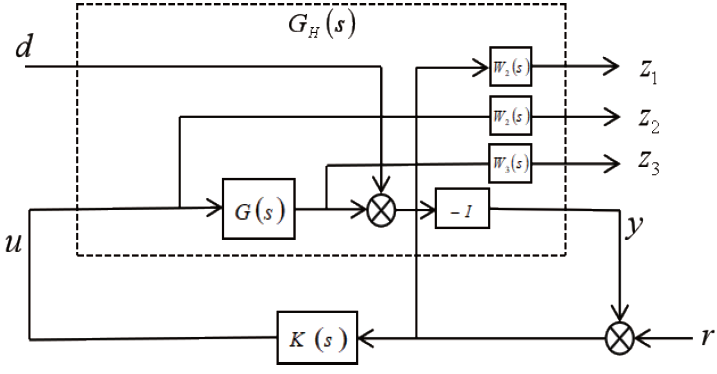
  应用混合灵敏度方法设计控制器时，加权阵的选取是重中之重，它决定了系统灵敏度函数和补灵敏度函数频域特性的形状，进而直接决定了总系统动态、稳态性能及鲁棒性的好坏。加权阵的选取需要遵循以下规则：1）最终设计的控制器和广义被控对象同阶，因此在满足设计的基本要求的情况下，尽可能降低加权阵的阶次。

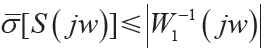
  为对象不确定性界函数，它决定了系统鲁棒边界，其幅频特性包含所有未建模动态，而未建模动态往往呈高频特性，因此其要求在低频增益小，高频增益大，并且其截止频率需大于

  控制器的时候需先进行双线性变换将虚轴极点移位，待设计好后在将以为极点还原，最终运用MATLAB 鲁棒控制工具箱中的hinfsyn 函数，得到的鲁棒控制器的形式为：

  控制下的系统开环传递函数曲线 中能够准确的看出，系统的截止频率ωc =149 rad / s，相位裕度为74.8°，满足精度和鲁棒稳定性要求。低频段系统表现为-60 dB/dec，这说明系统对阶跃响应必为无静差系统，具有很好的稳定性，并且由于系统低频段有较高的分贝值，能够保证系统的稳态精度；中频段以-20 dB/dec 穿过0 dB 线且具有一定的宽度，从相位裕度也能够准确的看出系统有较好的平稳性；在高频段系统表现为-60 dB/dec，这表明系统有较好的噪声抑制能力。

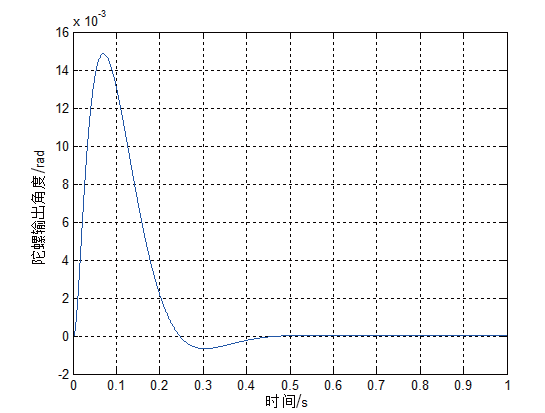
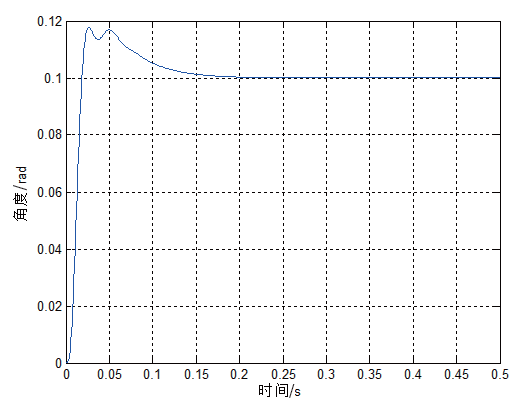
  控制稳定回路输入0.1 rad的阶跃信号和0.5 N·m 的干扰力矩，系统的响应曲线 能够准确的看出，采用H∞ 控制后，系统的超调量仅为13.7%，调节时间仅为0.089 s，当输入常值干扰力矩后，稳定回路的最大动态干扰误差为0.013 7 rad， 稳态误差趋于0。通过PID 控制和H

  控制的对比，能够准确的看出，系统的超调量超调量、调节时间和抗干扰能力都明显得到了明显改善。

  ∞混合灵敏度控制策略对液浮陀螺稳定回路来控制，通过选择正真适合的加权函数，使控制结果在跟踪和抗扰方面都有了显著的提高，通过仿真，验证了采用H∞

  [2] 申铁龙.H∞控制理论及应用[M].北京:清华大学出版社,1996.

  [6] ,孟卫锋,陈利超,等.惯导平台稳定回路三种控制策略的仿真研究[J].科学技术与工程,2010(3):672-676,691.（本文来源于《电子科技类产品世界》杂志2021年1月期）